题目描述
sjx同学天天在家摆烂,甚是无聊!于是,他发明了一种"跳跳球"游戏来打磨时间。
他将自己的房间用一个$n*m$的网格表示。在位置$(i_1,j_1)$($i_1$行和$j_1$列的交集)处有一个球,它开始沿四个对角线方向之一移动:
···球向右下方移动,记为$DR$,这就意味着走了一步后,球的位置从$(i,j)$变为$(i+1,j+1)$。
···球向左下方移动,记为$DL$,这就意味着走了一步后,球的位置从$(i,j)$变为$(i+1,j-1)$。
···球向右上方移动,记为$UR$,这就意味着走了一步后,球的位置从$(i,j)$变为$(i-1,j+1)$。
···球向左上方移动,记为$UL$,这就意味着走了一步后,球的位置从$(i,j)$变为$(i-1,j-1)$。
每走一步之后,球都会保持其方向,除非它撞到墙壁(也就是说,该方向的下一步将将球带出房间的边界)。在这种情况下,球的方向沿着墙的轴线翻转(遵循发射定律)。如果球的撞到房间的角落,两个方向都会翻转(如:左上翻转为右下)。任何这种情况都称为反弹。此外,球永远不会停止移动。
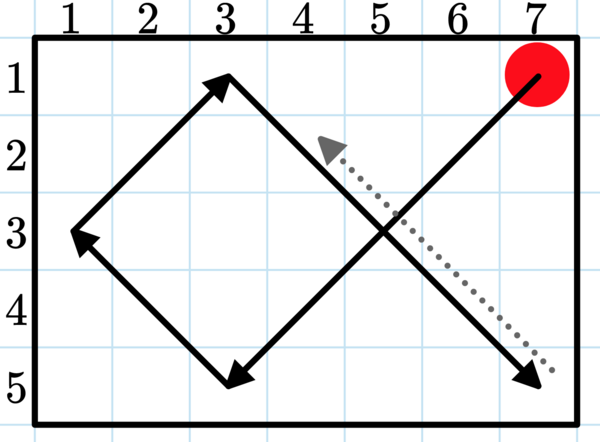
在上面的示例中,球从$(1,7)$开始,按$DL$方向行进,直到到达底墙,然后弹跳并继续朝$UL$方向运动。到达左侧墙壁后,球会弹起并继续朝$UR$方向移动。当球到达上墙时,它会弹起并继续朝$DR$方向移动。到达右下角后,它会弹一次并继续朝$UL$方向移动,依次类推。
sjx想知道当球到达房间中的单元格$(i_2,j_2)$时,球会经历多少次反弹。若球从未到达过单元格$(i_2,j_2)$,请输出$-1$。
注意,球首先在某个单元格中,然后只有在撞到墙壁后才会反弹。
他将自己的房间用一个$n*m$的网格表示。在位置$(i_1,j_1)$($i_1$行和$j_1$列的交集)处有一个球,它开始沿四个对角线方向之一移动:
···球向右下方移动,记为$DR$,这就意味着走了一步后,球的位置从$(i,j)$变为$(i+1,j+1)$。
···球向左下方移动,记为$DL$,这就意味着走了一步后,球的位置从$(i,j)$变为$(i+1,j-1)$。
···球向右上方移动,记为$UR$,这就意味着走了一步后,球的位置从$(i,j)$变为$(i-1,j+1)$。
···球向左上方移动,记为$UL$,这就意味着走了一步后,球的位置从$(i,j)$变为$(i-1,j-1)$。
每走一步之后,球都会保持其方向,除非它撞到墙壁(也就是说,该方向的下一步将将球带出房间的边界)。在这种情况下,球的方向沿着墙的轴线翻转(遵循发射定律)。如果球的撞到房间的角落,两个方向都会翻转(如:左上翻转为右下)。任何这种情况都称为反弹。此外,球永远不会停止移动。

在上面的示例中,球从$(1,7)$开始,按$DL$方向行进,直到到达底墙,然后弹跳并继续朝$UL$方向运动。到达左侧墙壁后,球会弹起并继续朝$UR$方向移动。当球到达上墙时,它会弹起并继续朝$DR$方向移动。到达右下角后,它会弹一次并继续朝$UL$方向移动,依次类推。
sjx想知道当球到达房间中的单元格$(i_2,j_2)$时,球会经历多少次反弹。若球从未到达过单元格$(i_2,j_2)$,请输出$-1$。
注意,球首先在某个单元格中,然后只有在撞到墙壁后才会反弹。
输入
第一行包含一个整数$t(1≤t≤50)$--测试用例的数量。
每个测试用例的第一行包含六个整数和一个字符串$n,m,i_1,j_1,i_2,j_2,d(2≤n,m≤25000;1≤i_1,i_2≤n;1≤j_1,j_2≤m;d∈(DR,DL,UR,UL))$--网格的尺寸,球的起始坐标,球的终止坐标和球的起始方向。
测试数据保证所有的测试用例的$n*m$之和不超过5·104。
每个测试用例的第一行包含六个整数和一个字符串$n,m,i_1,j_1,i_2,j_2,d(2≤n,m≤25000;1≤i_1,i_2≤n;1≤j_1,j_2≤m;d∈(DR,DL,UR,UL))$--网格的尺寸,球的起始坐标,球的终止坐标和球的起始方向。
测试数据保证所有的测试用例的$n*m$之和不超过5·104。
输出
对于每一个测试用例,输出一个整数--球第一次到达单元格$(i_2,j_2)$之间的弹跳次数。
如果球从未达到该点,则输出$-1$。
如果球从未达到该点,则输出$-1$。
样例输入 Copy
6
5 7 1 7 2 4 DL
5 7 1 7 3 2 DL
3 3 1 3 2 2 UR
2 4 2 1 2 2 DR
4 3 1 1 1 3 UL
6 4 1 2 3 4 DR
样例输出 Copy
3
-1
1
-1
4
0