题目描述
有一张 $(N_1 + N_2)$ 个点 $M$ 条边的无向图,且保证:
- 对于所有 $u, v \in [1, N_1]$,$u$ 点和 $v$ 点连通;
- 对于所有 $u, v \in [N_1 + 1, N_1+N_2]$,$u$ 点和 $v$ 点连通;
- $1$ 点和 $(N_1 + N_2)$ 点不连通。
现在你需要选择一个点 $u \in [1, N_1]$ 和一个点 $v \in [N_1 + 1, N_1+N_2]$,连接这两个点。
问连接后从 $1$ 点走到 $(N_1 + N_2)$ 点的最短路径(路径上的边数)最大是多少。
- 对于所有 $u, v \in [1, N_1]$,$u$ 点和 $v$ 点连通;
- 对于所有 $u, v \in [N_1 + 1, N_1+N_2]$,$u$ 点和 $v$ 点连通;
- $1$ 点和 $(N_1 + N_2)$ 点不连通。
现在你需要选择一个点 $u \in [1, N_1]$ 和一个点 $v \in [N_1 + 1, N_1+N_2]$,连接这两个点。
问连接后从 $1$ 点走到 $(N_1 + N_2)$ 点的最短路径(路径上的边数)最大是多少。
输入
第一行三个整数$N_1,N_2,M$分别表示第一个连通块内的点数,第二个连通块内的点数,以及$M$条边(无向边)
接下来$M$行,每行两个整数$u_i,v_i$表示$u_i,v_i$这两个点相连
接下来$M$行,每行两个整数$u_i,v_i$表示$u_i,v_i$这两个点相连
- $1 \leq N_1,N_2 \leq 1.5 \times 10^5$
- $0 \leq M \leq 3 \times 10^5$
- $1 \leq a_i \leq b_i \leq N_1+N_2$
- $(a_i,b_i) \neq (a_j,b_j)$ 如果 $i \neq j$ .(也就是说,图中没有重边)
- 数据保证:对于所有 $u, v \in [1, N_1]$,$u$ 点和 $v$ 点连通;对于所有 $u, v \in [N_1 + 1, N_1+N_2]$,$u$ 点和 $v$ 点连通; $1$ 点和 $(N_1 + N_2)$ 点不连通。
- 所有输入值均为整数。
输出
选择一个点 $u \in [1, N_1]$ 和一个点 $v \in [N_1 + 1, N_1+N_2]$,连接这两个点。
输出连接后从 $1$ 点走到 $(N_1 + N_2)$ 点的最短路径(路径上的边数)最大是多少。
输出连接后从 $1$ 点走到 $(N_1 + N_2)$ 点的最短路径(路径上的边数)最大是多少。
样例输入 Copy
3 4 6
1 2
2 3
4 5
4 6
1 3
6 7
样例输出 Copy
5
提示
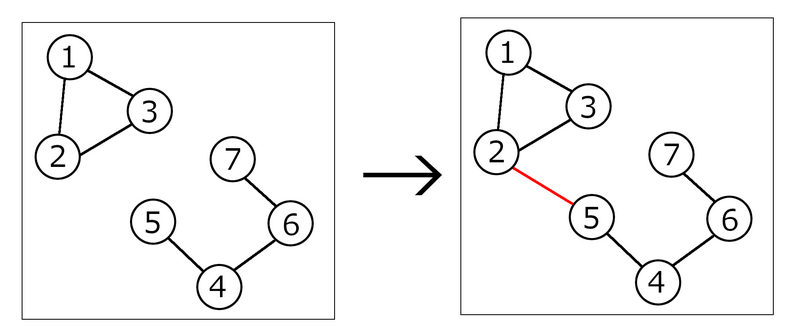
样例1图解: