xwc喜欢连在一起的数字，如果这些数字的和很大就更好了。

所以他现在要给你一个 $n$ 行 $n$ 列的网格 $A$，第 $i$ 行第 $j$ 列上填有一个整数 A_i,_j。

接下来你可以在 $A$ 上任取一行、一列或  一条与任意对角线（即两条斜着的对角线）平行且只经过网格交叉点  的直线（注意，不是线段），满足经过至少一个数字，且经过的数字之和最大。

如果对上面的表述有疑惑，请参考样例解释辅助理解。

你需要告诉xwc这个最大的数字之和。

输入共 $n+1$ 行。

第一行，一个正整数 $n$，表示方阵的行数、列数。
接下来 $n$ 行，每行 $n$ 个用空格隔开的整数，其中第 $i$ 行第 $j$ 个整数表示$Ai,j$。

输出一行一个整数，表示最大的数字之和。

样例输入 #2

3
-1 1 2
4 0 3
1 9 2

样例输出 #2

13

---

样例输入 #3

3
-1 -1 -1
-1 -1 -1
-1 -1 -1

样例输出 #3

-1

---

样例输入 #4

3
-100 -10 -100
-10 99999 -10
-100 -10 -100

样例输出 #4

99979

---

样例输入 #5

3
1 2 3
1 3 2
3 2 1

样例输出 #5

9

---

样例解释

样例 1 解释

对于样例 $1$，不难看出第 $3$ 行数字之和最大，有 $3+3+3=9$。

样例 2 解释

对于样例 $2$，数字之和最大的，满足条件的线如下所示：

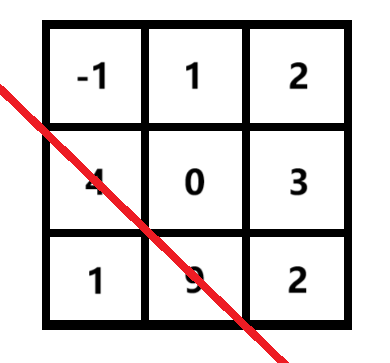
此时有 $4+9=13$。

注意，因为要求与对角线平行的直线只能经过网格交点，所以并不能出现同时取 $4,1,9$ 或同时取 $4,1,9,2$ 这样的情况。

样例 $3$ 解释

取某条只经过一个 $-1$ 的直线即为最大。注意，不可以一个数字都不选。

样例 $4$ 解释

显然，取斜着的线一定不优，只能选择中间那一行或一列，答案是 $-10+99999-10=99979$。

样例 5 解释

满足条件的线显然如图所示: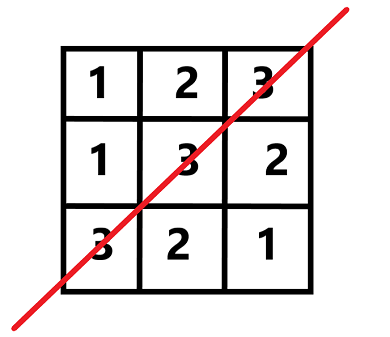

数据范围

对于 $100\%$ 的数据，保证 1≤n≤1×10³,−10³≤ A_i,_j≤10³。